Cho tam giác ABC, M là điểm trên cạnh BC. Qua B, C dựng các đường thẳng song song với AM cắt AC, AB lần lượt tại P, Q

Hướng dẫn giải:

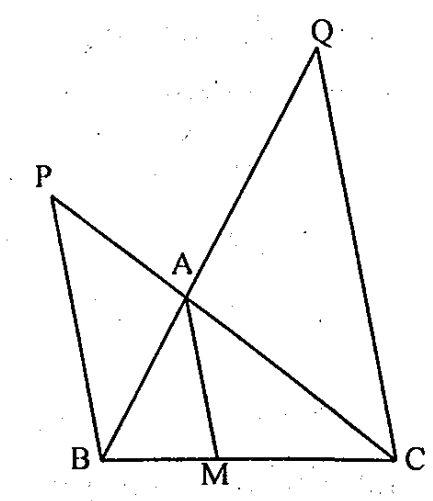
Theo giả thiết  \( AM\parallel PB\parallel QC \), theo định lí Thales

 \( \Rightarrow \frac{AM}{PB}=\frac{CM}{CB} \) và  \( \frac{AM}{QC}=\frac{BM}{BC} \), cộng hai vế ta có:  \( \frac{AM}{PB}+\frac{AM}{QC}=\frac{CM}{CB}+\frac{BM}{BC}=\frac{BM+MC}{BC}=\frac{BC}{BC}=1 \)

 \( \Rightarrow \frac{1}{AM}=\frac{1}{PB}+\frac{1}{QC} \).