Cho tứ giác ABCD và I, J trung điểm của AD và BC. Gọi G, E là trọng tâm tam giác ABC và ABD. Chứng minh rằng DG, CE, IJ đồng quy, từ đó suy ra GE song song với CD

Hướng dẫn giải:

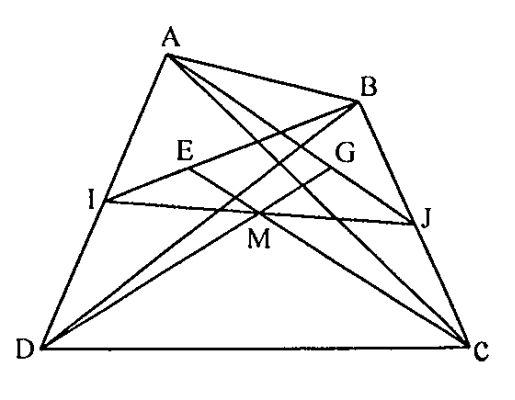
G là trọng tâm của  \( \Delta ABC\Rightarrow AG=2GJ \).

Áp dụng định lí Menelaus với  \( \Delta AIJ \), đường thẳng DG cắt tại M  \( \Rightarrow \frac{DA}{DI}.\frac{MI}{MJ}.\frac{GJ}{GA}=1 \).

 \( IA=ID\Rightarrow DA=2DI\Rightarrow 2.\frac{MI}{MJ}.\frac{1}{2}=1 \).

 \( \Rightarrow MI=MJ \), E là trọng tâm  \( \Delta ABD \), hoàn toàn tương tự

 \( \Rightarrow CE \) đi qua trung điểm của IJ  \( \Rightarrow \)  ba đường thẳng DG, CE, IJ đồng quy.

Áp dụng định lí Menelaus với  \( \Delta ADG \), ứng với ba điểm M, I, J thẳng hàng

 \( \Rightarrow \frac{IA}{ID}.\frac{MD}{MG}.\frac{JG}{JA}=1\Rightarrow \frac{MD}{MG}.\frac{1}{3}=1\Rightarrow \frac{MD}{MG}=3 \), tương tự  \( \Rightarrow \frac{MC}{ME}=3 \).

 \( \Rightarrow \frac{MD}{MG}=\frac{MC}{ME} \), theo định lí Thales thì EG song song với CD.