Cho 6 điểm A, B, C, D, E, F nằm trên đường tròn. AE cắt DF tại M, BE cắt CF tại I và AC cắt BD tại N. Chứng minh rằng M, I, N thẳng hàng.
Hướng dẫn giải:
Lời giải:
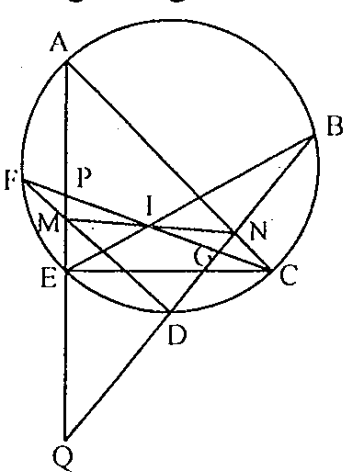
Giả sử đường thẳng AE cắt đường thẳng CF và BD lần lượt tại P, Q. Đường thẳng BD cắt CF tại G. Áp dụng định lí Menelaus trong \( \Delta PQG \) với các cát tuyến MFD, IEB, NAC ta có:
\( \frac{FP}{FG}.\frac{DG}{DQ}.\frac{MQ}{MP}=1\Rightarrow \frac{MQ}{MP}=\frac{FG}{FP}.\frac{DQ}{DG} \).
\( \frac{BG}{BQ}.\frac{EQ}{EP}.\frac{IP}{IG}=1\Rightarrow \frac{IP}{IG}.\frac{BQ}{BG}.\frac{EP}{EQ} \) và \( \frac{NG}{NQ}.\frac{AQ}{AP}.\frac{CP}{CG}=1\Rightarrow \frac{NG}{NQ}=\frac{AP}{AQ}.\frac{CG}{CP} \).
Nhân ba đẳng thức với nhau, ta có:
\( \frac{MQ}{MP}.\frac{IP}{IG}.\frac{NG}{NQ}=\frac{FG}{FP}.\frac{DQ}{DG}.\frac{BQ}{BG}.\frac{EP}{EQ}.\frac{AP}{AQ}.\frac{CG}{CP} \) (*)
Mặt khác, cát tuyến AE, CF cắt nhau tại P \( \Rightarrow PA.PE=PC.PF \);
Tương tự \( QD.QB=QE.QA \) và \( GF.GC=GD.GB \), thay vào đẳng thức (*)
\( \Rightarrow \frac{MQ}{MP}.\frac{IP}{IG}.\frac{NG}{NQ}=1\Rightarrow M,I,N \) thẳng hàng.
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
No comment yet, add your voice below!