Cho tam giác ABC nội tiếp đường tròn (O), AD là phân giác của tam giác, M là điểm thay đổi trên AD, P và Q là hình chiếu của M trên AB và AC, I là trung điểm BC, H là hình chiếu của I trên PQ

Hướng dẫn giải:

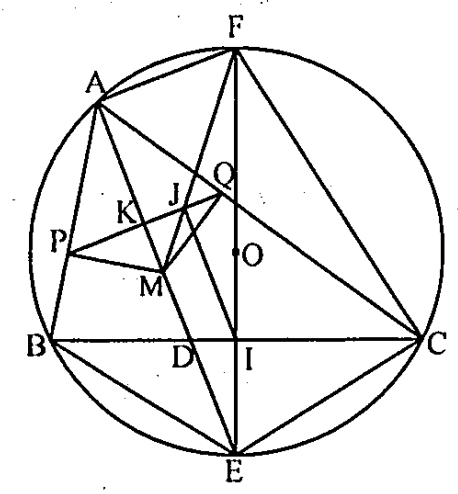
AD cắt đường tròn (O) tại E  \( \Rightarrow EC=EB \)

 \( \Rightarrow EI \) là đường thẳng chứa một đường kính của đường tròn (O) cố định, đường kính này cắt (O) tại F.

 \( \Rightarrow F \) là điểm cố định.

Giả sử MF cắt PQ tại J. Theo giả thiết ta có  \( \widehat{PAM}=\widehat{QAM} \), \(MP\bot AB,\text{ }MQ\bot AC\)

 \( \Rightarrow AM\bot PQ \).

Gọi K là giao điểm AM và PQ, EF là đường kính.

 \( \Rightarrow \widehat{ECF}={{90}^{O}},\widehat{EFC}=\widehat{EAC} \) (chắn cung  \( \overset\frown{CE} \))

 \( \Rightarrow \Delta AQM\backsim \Delta FCE \) (g.g) \( \Rightarrow \frac{FI}{IE}=\frac{AK}{KM} \)  (1)

Mặt khác EF là đường kính nên  \( AE\bot AF\Rightarrow AF\parallel PQ\Rightarrow \frac{AK}{KM}=\frac{FJ}{JM} \)  (2)

Từ (1) và (2)  \( \Rightarrow \frac{FI}{IE}=\frac{FJ}{JM} \), theo định lí Thales đảo  \( \Rightarrow IJ\parallel AD \).

 \( \Rightarrow IJ\bot PQ\Rightarrow J\equiv H\Rightarrow MH \) luôn đi qua F là điểm cố định.