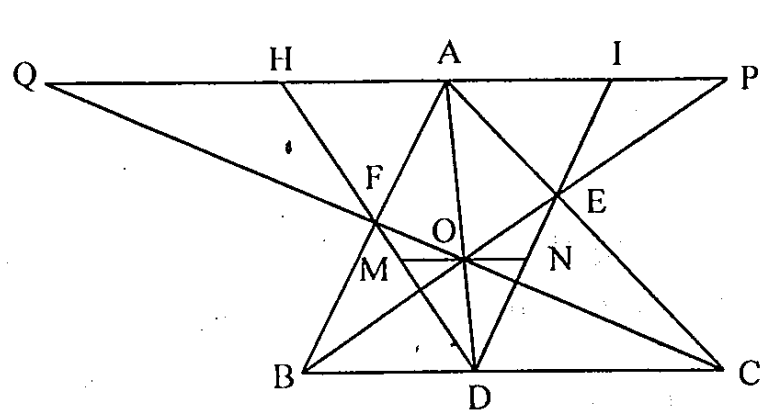
Cho tam giác nhọn ABC, gọi (O1), (O2) là tâm đường tròn bàng tiếp của tam giác ứng với góc \( \widehat{B} \) và \( \widehat{C} \). Đường tròn (O1) tiếp xúc với cạnh BC, AB, CA tại M, N, E đường tròn (O2) tiếp xúc với cạnh BC, AC, AB tại P, Q, F; đường thẳng MN và PQ cắt nhau tại D. Chứng minh rằng AD vuông góc với BC.
Hướng dẫn giải:

Theo giả thiết đường tròn (O1) tiếp xúc AC tại E, AB tại N suy ra \( {{O}_{1}}N\bot AB \), \( {{O}_{1}}E\bot AC \) \( \Rightarrow \widehat{{{O}_{1}}AN}=\widehat{{{O}_{1}}AE} \);
Đường tròn (O2) tiếp xúc AB tại F và AC tại Q suy ra \( {{O}_{2}}Q\bot AC \), \( {{O}_{2}}F\bot AB \).
\( \Rightarrow \widehat{{{O}_{2}}AQ}=\widehat{{{O}_{2}}AF}\Rightarrow \widehat{{{O}_{1}}AN}=\widehat{{{O}_{2}}AF}\Rightarrow {{O}_{1}},A,{{O}_{2}} \) thẳng hàng.
\( \Rightarrow \Delta {{O}_{2}}QA\backsim \Delta {{O}_{1}}NA \) (g.g) \( \Rightarrow \frac{AN}{AQ}=\frac{{{O}_{1}}A}{{{O}_{2}}A} \) (1)
Theo giả thiết \( {{O}_{1}}M\bot BC,\text{ }{{O}_{2}}P\bot BC \).
\( \Rightarrow \frac{PH}{MH}=\frac{{{S}_{DPH}}}{{{S}_{MDH}}}=\frac{DP\sin \widehat{PDH}}{DM\sin \widehat{MDH}} \).
Mặt khác, áp dụng định lí sin cho \( \Delta ABC \):
\( \frac{DP}{DM}=\frac{\sin \widehat{DMP}}{\sin \widehat{DPM}}=\frac{\cos \widehat{{{O}_{1}}MN}}{\cos \widehat{{{O}_{2}}PQ}}=\frac{\sin \widehat{MNA}}{\sin \widehat{PQA}}=\frac{\sin \widehat{DNA}}{\sin \widehat{DQA}} \).
Áp dụng tiếp định lí sin cho \( \Delta DNA \) và \( \Delta DQA \), ta được:
\( \frac{PH}{MH}=\frac{\sin \widehat{DNA}\sin \widehat{PDH}}{\sin \widehat{DQA}\sin \widehat{MDH}}=\frac{\sin \widehat{DNA}}{\sin \widehat{MDH}}.\frac{\sin \widehat{PDH}}{\sin \widehat{DQA}} \)
\( =\frac{\sin \widehat{DNA}}{\sin \widehat{NDA}}.\frac{\sin \widehat{QDA}}{\sin \widehat{DQA}}=\frac{DA}{AN}.\frac{AQ}{DA}=\frac{AQ}{AN} \).
Kết hợp (1) \( \Rightarrow \frac{PH}{MH}=\frac{{{O}_{2}}A}{{{O}_{1}}A}\Rightarrow {{O}_{2}}P\parallel DH\parallel {{O}_{1}}M\Rightarrow DH\bot BC \).
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng