Cho hình chóp tứ giác đều S.ABCD độ dài cạnh đáy là a. Biết rằng mặt phẳng (P) qua A và vuông góc với SC, cắt cạnh SB tại B’ với \( \frac{SB’}{SB}=\frac{2}{3} \). Tính thể tích của khối chóp S.ABCD
A. \( \frac{{{a}^{3}}\sqrt{6}}{6} \)
B. \( \frac{{{a}^{3}}\sqrt{6}}{4} \)
C. \( \frac{{{a}^{3}}\sqrt{6}}{2} \)
D. \( \frac{{{a}^{3}}\sqrt{6}}{3} \)
Hướng dẫn giải:
Đáp án A.
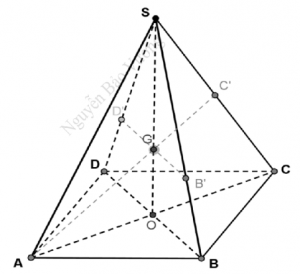
Ta có: \( \left. \begin{align} & BD\bot AC \\ & BD\bot SO \\ \end{align} \right\}\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot SC \)
Mà \( \left( P \right)\bot SC\Rightarrow \left( P \right)//BD \)
Trong (SAC), gọi \( G=A’C\cap SO\Rightarrow GB’//BD \) \( \Rightarrow \frac{SG}{SO}=\frac{SB’}{SB}=\frac{2}{3} \)
Suy ra G là trọng tâm \( \Delta SAC \) \( \Rightarrow C’ \) là trung điểm SC.
Nên \( \Delta SAC \) là tam giác đều cạnh \( AC=a\sqrt{2}\Rightarrow SO=a\sqrt{2}.\frac{\sqrt{3}}{2}=\frac{a\sqrt{6}}{2} \)
\( \Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{3}{{a}^{2}}.\frac{a\sqrt{6}}{2}=\frac{{{a}^{3}}\sqrt{6}}{6} \)
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
No comment yet, add your voice below!