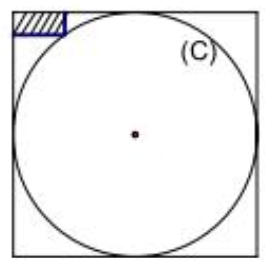
Cho hình trụ (T) có (C) và (C’) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước \( a\times 2a \) (như hình vẽ dưới đây). Tính thể tích V của khối trụ (T) theo a.
A. \( \frac{100\pi {{a}^{3}}}{3} \).
B. \( 250\pi {{a}^{3}} \).
C. \( \frac{250\pi {{a}^{3}}}{3} \).
D. \( 100\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn B

Ta có \( BK=2a,\,\,KI=a \) nên \( BI=a\sqrt{5}\Rightarrow \cos \widehat{KBI}=\frac{1}{\sqrt{5}} \) và \( \sin \widehat{KBI}=\frac{2}{\sqrt{5}} \).
Khi đó \( \cos \widehat{OBI}=\cos \left( \widehat{KBI}-\widehat{KBO} \right)=\cos \widehat{KBI}.\cos 45{}^\circ +\sin \widehat{KBI}.\sin 45{}^\circ \)
\( =\frac{1}{\sqrt{5}}.\frac{\sqrt{2}}{2}+\frac{2}{\sqrt{5}}.\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2\sqrt{5}} \).
Kí hiệu \( AB=2x \) thì \( OI=x,\,\,OB=x\sqrt{2} \).
Ta có: \( O{{I}^{2}}=B{{O}^{2}}+B{{I}^{2}}-2.BO.BI.\cos \widehat{OBI}=2{{x}^{2}}+5{{a}^{2}}-2.x\sqrt{2}.a\sqrt{5}.\frac{3\sqrt{2}}{2\sqrt{5}}=2{{x}^{2}}+5{{a}^{2}}-6xa \)
\( \Leftrightarrow {{x}^{2}}=2{{x}^{2}}+5{{a}^{2}}-6xa\Leftrightarrow {{x}^{2}}-6xa+5{{a}^{2}}=0\Leftrightarrow \left[ \begin{align} & x=a \\ & x=5a \\ \end{align} \right. \).
Vì \( x>a \) nên \( x=5a \) hay \( r=OI=5a \).
Vậy thể tích khối trụ (T) là \( V=\pi .{{(5a)}^{2}}.10a=250\pi {{a}^{3}} \).
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Dạy kèm môn Toán Cao Cấp - Xác suất thống kê
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
No comment yet, add your voice below!