Cho hình chóp đều S.ABC có SA = a. Gọi D, E lần lượt là trung điểm của SA, SC. Tính thể tích khối chóp S.ABC theo a, biết BD vuông góc với AE.
A. \(\frac{{{a}^{3}}\sqrt{21}}{54}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{12}\)
C. \(\frac{{{a}^{3}}\sqrt{7}}{27}\)
D. \(\frac{{{a}^{3}}\sqrt{21}}{27}\)
Hướng dẫn giải:
Đáp án A.
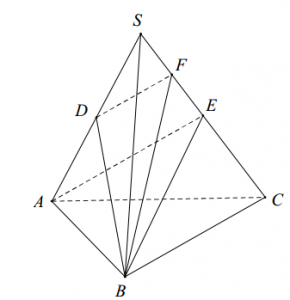
Gọi F là trung điểm SE \( \Rightarrow BD\bot DF \)
Gọi AB = x.
Ta có: \( B{{E}^{2}}=B{{D}^{2}}=A{{E}^{2}}=\frac{2A{{S}^{2}}+2A{{C}^{2}}-S{{C}^{2}}}{4}\) \( =\frac{2{{a}^{2}}+2{{x}^{2}}-{{a}^{2}}}{4}=\frac{{{a}^{2}}+2{{x}^{2}}}{4} \)
\( B{{F}^{2}}=\frac{2B{{S}^{2}}+2B{{E}^{2}}-S{{E}^{2}}}{4} \) \( =\frac{2{{a}^{2}}+\frac{{{a}^{2}}+2{{x}^{2}}}{2}-\frac{1}{4}{{a}^{2}}}{4}=\frac{9{{a}^{2}}+4{{x}^{2}}}{16} \)
\( B{{F}^{2}}=B{{D}^{2}}+D{{F}^{2}}\Leftrightarrow B{{F}^{2}}=\frac{5B{{D}^{2}}}{4} \) \( \Leftrightarrow \frac{9{{a}^{2}}+4{{x}^{2}}}{16}=\frac{5}{4}.\frac{{{a}^{2}}+2{{x}^{2}}}{4} \)
\( \Leftrightarrow 9{{a}^{2}}+4{{x}^{2}}=5{{a}^{2}}+10{{x}^{2}}\Leftrightarrow 4{{a}^{2}}=6{{x}^{2}} \) \( \Rightarrow x=a\sqrt{\frac{2}{3}} \)
Gọi H là hình chiếu của S lên (ABC) khi đó H là tâm đường tròn ngoại tiếp \( \Delta ABC \)
\( \Rightarrow SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{2}{3}.\frac{x\sqrt{3}}{2} \right)}^{2}}}=\frac{a\sqrt{7}}{3} \)
Tam giác ABC đều có cạnh là x \( \Rightarrow {{S}_{\Delta ABC}}=\frac{{{x}^{2}}\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{6} \)
Vậy \( {{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{\Delta ABC}} \) \( =\frac{1}{3}.\frac{a\sqrt{7}}{3}.\frac{{{a}^{2}}\sqrt{3}}{6}=\frac{{{a}^{3}}\sqrt{21}}{54} \)
Hoặc sử dụng công thức tính thể tích chóp tam giác ABC đều có cạnh bên bằng a, cạnh đáy bằng x.
\( {{V}_{S.ABC}}=\frac{{{x}^{2}}\sqrt{3{{a}^{2}}-{{x}^{2}}}}{12}=\frac{\frac{2{{a}^{2}}}{3}\sqrt{3{{a}^{2}}-\frac{2{{a}^{2}}}{3}}}{12}=\frac{{{a}^{3}}\sqrt{21}}{54} \)
Các bài toán liên quan
Các bài toán mới!
Các sách tham khảo do Trung Tâm Nhân Tài Việt phát hành!
Thông Tin Hỗ Trợ Thêm!
- Với đội ngũ gia sư dạy kèm gồm giáo viên và sinh viên ở các trường uy tín nhất, chúng tôi nhận dạy kèm tại nhà và dạy kèm online 1 kèm 1.
- Nhận dạy kèm môn phổ thông: Toán học, Vật lý, Hóa học, Tiếng Anh, Sinh học, Văn học, … các lớp 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, LTDH và các môn ĐH–CĐ: Toán cao cấp, Xác suất thống kê...
- Nhận dạy kèm Tiếng Anh (Giao tiếp, TOEIC, TOEFL, IELTS, ...) - Tiếng Hoa - Tiếng Hàn - Tiếng Nhật (Giao tiếp, chứng chỉ N5, N4, N3, N2, N1), Tin Học (Văn phòng, Đồ họa, Lập trình,...) cho các học viên ở mọi lứa tuổi.
- Nhận dạy kèm các môn năng khiếu: Cờ Vua, Cờ Tướng, Đàn Ghitar, Đàn Dương Cầm,…
- Đ/C Trung Tâm: Số 103/6, Hẻm 528TC, Đường Trường Chinh, Kp. 7, P. Tân Hưng Thuận, Quận 12, Tp. HCM
- Hotline: 094.625.1920 - Thầy Nhân (Zalo)
No comment yet, add your voice below!