cho mặt phẳng (P):x+y−z−3=0 và hai điểm M(1;1;1), N(-3;-3;-3). Mặt cầu (S) đi qua M, N và tiếp xúc với mặt phẳng (P) tại điểm Q. Biết rằng Q luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.

Hướng dẫn giải:

Chọn B

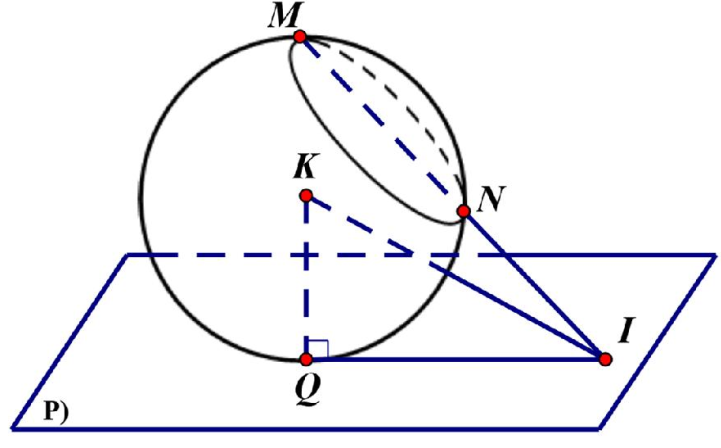
+ Đường thẳng MN có phương trình là  \( MN:\left\{ \begin{align}  & x=1+t \\  & y=1+t \\  & z=1+t \\ \end{align} \right. \).

+ Gọi  \( I=MN\cap (P) \) khi đó tọa độ điểm I ứng với t thỏa mãn:

 \( 1+t+1+t-1-t-3=0\Leftrightarrow t-2=0\Leftrightarrow t=2\Rightarrow I(3;3;3)\Rightarrow IM=2\sqrt{3},\text{ }IN=6\sqrt{3} \).

+ Do mặt cầu (S) đi qua M, N và tiếp xúc với đường thẳng IQ tại điểm Q nên ta có:

 \( I{{Q}^{2}}=IM.IN=K{{I}^{2}}-{{R}^{2}}\Rightarrow I{{Q}^{2}}=IM.IN=36\Rightarrow IQ=6 \).

Vậy Q luôn thuộc đường tròn tâm I, bán kính  \( R=6 \).