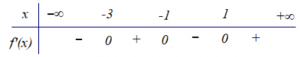
Hàm số y=f(3-2x) đồng biến trên khoảng

Hướng dẫn giải:

 Đáp án D.

Ta có:  \( {y}’=2{f}'(3-2x)\ge 0\Leftrightarrow {f}'(3-2x)\le 0 \)

 \( \Leftrightarrow \left[ \begin{align}& 3-2x\le -3 \\& -1\le 3-2x\le 1 \\\end{align} \right. \) \( \Leftrightarrow \left[ \begin{align}& x\ge 3 \\& 1\le x\le 2 \\\end{align} \right. \)