Cho hàm số f(x) có đạo hàm liên tục trên \( \mathbb{R} \) và \( f(0)<0 \), đồ thị của \( {f}'(x) \) như hình vẽ:
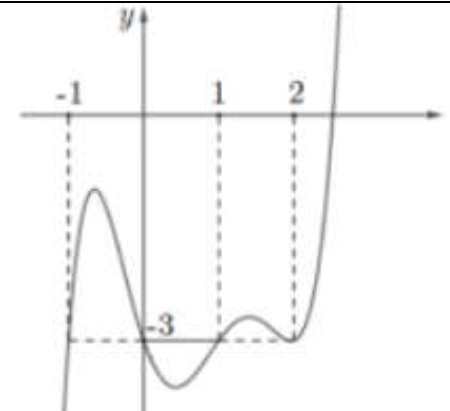
Gọi m, n lần lượt là số điểm cực đại, số điểm cực tiểu của hàm số \( g(x)=\left| f\left( \left| x \right| \right)+3\left| x \right| \right| \). Giá trị của \( {{m}^{n}} \) bằng:
A. 4.
B. 8.
C. 27.
D. 16.
Hướng dẫn giải:
Chọn B
Xét hàm số \( u(x)=f\left( \left| x \right| \right)+3\left| x \right| \) là một hàm số chẵn nên chỉ cần xét trên \( \left[ 0;+\infty \right) \) để suy ra bảng biến thiên của \( u(x) \) trên cả \( \mathbb{R} \).
Với \( x\ge 0\Rightarrow u(x)=f(x)+3x\Rightarrow {u}'(x)={f}'(x)+3=0\Leftrightarrow {f}'(x)=-3\xrightarrow{x\ge 0}x=0;x=1;x=2 \).
Bảng biến thiên:

Trong đó \( u(-1)=u(1)=f(1)+3;\text{ }u(0)=f(0)<0 \).
Suy ra \( g(x)=\left| u(x) \right| \) có tất cả 5 điểm cực trị trong đó 2 điểm cực đại và 3 điểm cực tiểu.
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
No comment yet, add your voice below!