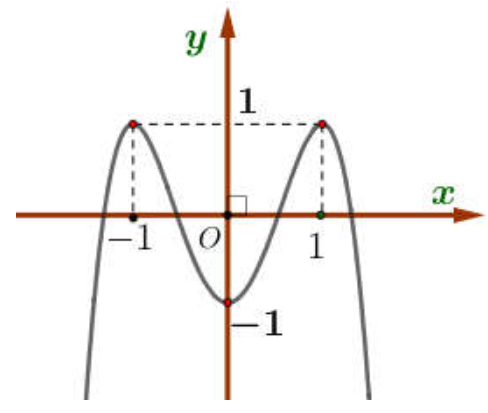
Cho hàm số \( y=f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d \) có bảng biến thiên như sau:

Tìm m để phương trình \( \left| f(x-1)+2 \right|=m \) có 4 nghiệm thỏa mãn \( {{x}_{1}}<{{x}_{2}}<{{x}_{3}}<1<{{x}_{4}} \).
A. \( 4<m<6 \).
B. \( 3<m<6 \).
C. \( 2<m<6 \).
D. \( 2<m<4 \).
Hướng dẫn giải:
Chọn A
Đồ thị hàm số \( y=\left| f(x-1)+2 \right| \) thu được bằng cách biến đổi đồ thị như sau:
+ Tịnh tiến đồ thị hàm số \( y=f(x) \) sang phải 1 đơn vị, sau đó tịnh tiến lên trên 2 đơn vị ta được đồ thị hàm số \( y=f(x-1)+2 \);
+ Với đồ thị hàm số \( y=\left| f(x-1)+2 \right| \): Giữa nguyên phần nằm bên trên trục hoành, lấy đối xứng phần nằm bên dưới trục hoành qua trục hoành rồi xóa phần nằm bên dưới trục hoành đi.
Do đó ta có bảng biến thiên:

Dựa vào bảng biến thiên, ta suy ra: \( 4<m<6 \).
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng