Cho hai số phức z và w thỏa mãn \( z+2w=8-6i \) và \( \left| z-w \right|=4 \). Giá trị lớn nhất của biểu thức \( \left| z \right|+\left| w \right| \) bằng
A. \( 4\sqrt{6} \)
B. \( 2\sqrt{26} \)
C. \( \sqrt{66} \)
D. \( 3\sqrt{6} \)
Hướng dẫn giải:
Đáp án C.
Giả sử M, N lần lượt là các điểm biểu diễn cho z và w. Suy ra: \( \overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{OF}=2\overrightarrow{OI} \), \( \left| z-w \right|=MN=4 \) và \( OF=2OI=10 \).
Đặt \( \left| z \right|=ON=\frac{a}{2};\text{ }\left| w \right|=OM=b \). Dựng hình bình hành OMFE.
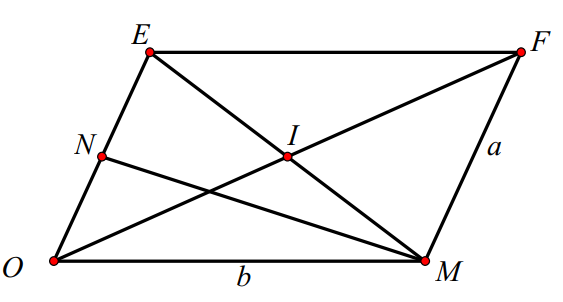
Ta có: \( \left\{ \begin{align} & \frac{{{a}^{2}}+{{b}^{2}}}{2}-\frac{M{{E}^{2}}}{4}=25 \\ & \frac{{{b}^{2}}+M{{E}^{2}}}{2}-\frac{{{a}^{2}}}{4}=16 \\ \end{align} \right.\Rightarrow {{a}^{2}}+2{{b}^{2}}=\frac{264}{3} \)
\( {{\left( \left| z \right|+\left| w \right| \right)}^{2}}={{\left( \frac{a}{2}+b \right)}^{2}}\le \left( {{a}^{2}}+2{{b}^{2}} \right)\left( \frac{1}{4}+\frac{1}{2} \right)=66 \).
Suy ra: \( a+b\le \sqrt{66} \), dấu “=” xảy ra khi \( a=b=\frac{2\sqrt{66}}{3} \).
Vậy \( {{(a+b)}_{\max }}=\sqrt{66} \).
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
No comment yet, add your voice below!