Biết rằng hai số phức z1, z2 thỏa mãn \( \left| {{z}_{1}}-3-4i \right|=1 \) và \( \left| {{z}_{2}}-3-4i \right|=\frac{1}{2} \). Số phức z có phần thực là a và phần ảo là b thỏa mãn \( 3a-2b=12 \). Giá trị nhỏ nhất của \( P=\left| z-{{z}_{1}} \right|+\left| z-2{{z}_{2}} \right|+2 \) bằng
A. \( {{P}_{\min }}=\frac{\sqrt{9945}}{11} \)
B. \( {{P}_{\min }}=5-2\sqrt{3} \)
C. \( {{P}_{\min }}=\frac{\sqrt{9945}}{13} \)
D. \( {{P}_{\min }}=5+2\sqrt{5} \)
Hướng dẫn giải:
Chọn C

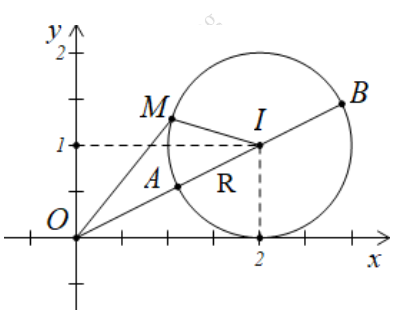
Gọi M1, M2, M lần lượt là điểm biểu diễn cho số phức z1, 2z2, z trên hệ tọa độ Oxy. Khi đó quỹ tích của điểm M1 là đường tròn (C1) tâm I(3;4), bán kính R = 1; quỹ tích của điểm M2 là đường tròn (C2) tâm I(6;8), bán kính R= 1; quỹ tích của điểm M à đường thẳng \( d:3x-2y-12=0 \).
Bài toán trở thành tìm giá trị nhỏ nhất của \( M{{M}_{1}}+M{{M}_{2}}+2 \).
Gọi (C3) có tâm \( {{I}_{3}}\left( \frac{138}{13};\frac{64}{13} \right),\text{ }R=1 \) là đường tròn đối xứng với (C2) qua d. Khi đó \( {{\left( M{{M}_{1}}+M{{M}_{2}}+2 \right)}_{\min }}={{\left( M{{M}_{1}}+M{{M}_{3}}+2 \right)}_{\min }} \) với \( {{M}_{3}}\in ({{C}_{3}}) \).
Gọi A, B lần lượt là giao điểm của đoạn thẳng \( {{I}_{1}}{{I}_{3}} \) với (C1), (C3). Khi đó với mọi điểm \( {{M}_{1}}\in ({{C}_{1}}),{{M}_{3}}\in ({{C}_{3}}),M\in d \) ta có: \( M{{M}_{1}}+M{{M}_{3}}+2\ge AB+2 \), dấu “=” xảy ra khi \( {{M}_{1}}\equiv A,\text{ }{{M}_{3}}\equiv B \).
Do đó: \( {{P}_{\min }}=AB+2={{I}_{1}}{{I}_{3}}-2+2={{I}_{1}}{{I}_{3}}=\frac{\sqrt{9945}}{13} \).
Nhận Dạy Kèm Môn Toán Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Môn Toán từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng